제목에서 말한 '컴퓨팅 플랫폼'이란 CPU, GPU, FPGA 등을 말한다.
이 들은 digital logic을 구성하며 2 진법 '0'과 '1' 만으로 기계를 작동시킨다.
즉, 컴퓨터는 2진수의 바다다.
2진수로 모든 숫자를 표현하고 연산을 수행한다.

2021.06.16 - [생각 미로] - [생각 미로] How do you define the real? - 영화 매트릭스
하지만 인간이 다루는 세계는 10진수로 통용되며 컴퓨터 위에 올려 사용하는 Application code 또한 10진법으로 사용한다.
그렇게 구현 시킨 Application code를 컴퓨터 하드웨어 단에서 동작시키려면 2진법으로 변환하여 연산하는 방법을 알아야 한다.
그래서 이번 포스팅에서는 컴퓨팅 플랫폼에서 10진수로 받은 값을 어떻게 2진수로 변환하여 사용하는 지에 대해 알아보고자 한다.
컴퓨팅 플랫폼은 어떻게 숫자를 다루나? (Feat. CPU)
컴퓨팅 플랫폼 예시로 CPU를 들면, CPU에는 연산 처리를 하는 요소가 있다.
이름은 ALU로 Arithmetic Logic Unit 의 약자이다.

이 안에서 크게 산술(Arithmetic) 연산과 논리(Logic) 연산이 이루어진다.
산술 연산은 덧셈, 뺄셈, 곱셈, 나눗셈이며 논리 연산은 OR, AND, NOT, XOR이 되겠다.
위에서 언급했던 10진수로 받아온 값을 여기서는 2진수로 변환되어 연산이 수행된다.
10진수 -> 2진수로 변환
#부동 소수점(Floating point) #IEEE 754 표준
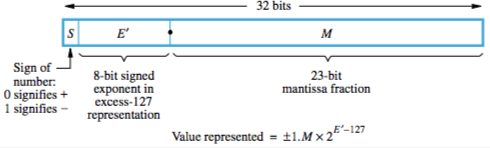
이 규격에 맞춰서 숫자를 변환한다.
S(Sign, 부호), E(Exponent, 2의 승수), M(Mantissa, 값)
(-1)^S x 0.1M x 2^E
M은 값의 정밀도를 나타내고 E는 값의 크기를 나타낸다.
예를 들어 13.625를 2진수로 표현한다면,
13.625(10) = 1101.101(2) = 0.1101101 x 2^4 로 나타낼 수 있다.
소수점 위의 13은 1101(2) 이며,
소수점 아래의 0.625는 1x2^(-1) + 0x2^(-2) + 1x2^(-3) = 0.625 로 표현할 수 있다.
그리고 위의 규격에 맞추어 표현하면 0.1101101 x 2^4 이 되는 것이다.
그럼 여기서 S는 0, M은 101101, E는 4라는 것을 알 수 있다.
이걸 32bit 기준으로 표기하면 '0 0000 0100 101 1010 0000 0000 0000 0000' 가 된다.
내가 만약 더 넓은 범위를 숫자를 표기하고 싶다면 32bit가 아닌 64bit로 늘리면 된다.
그럼 값의 크기를 나타내는 E의 bit 수가 많아져 표현할 수 있는 값의 범위가 넓어진다. 물론 M도 커져 표현할 수 있는 값의 세밀도가 올라간다.
여기서 말하는 32, 64 bit은 우리가 컴퓨터 사용할 때 0S 사양에 포함되는 그 값이다.
Window XP 시절까지는 32bit를 사용했지만 현재는 64bit를 대세로 사용하고 있다.
그럼 이렇게 변환한 2진수를 가지고 연산을 수행해보자.
논리(Logic) 연산
산술 연산에는 논리 연산이 사용되기 때문에 논리 연산에 대해 먼저 알아보도록 하겠다.
논리 연산은 디지털 연산에서 기본이 되는 요소라 논리가 비교적 간단하다.
Logic operations
아래 그림에서 보듯이 기능별로 symbol 형태가 다르며 Input A,B 값에 의해 Output Y 값이 출력된다.
(이 부분은 기본이라 외우는 단계이다.)
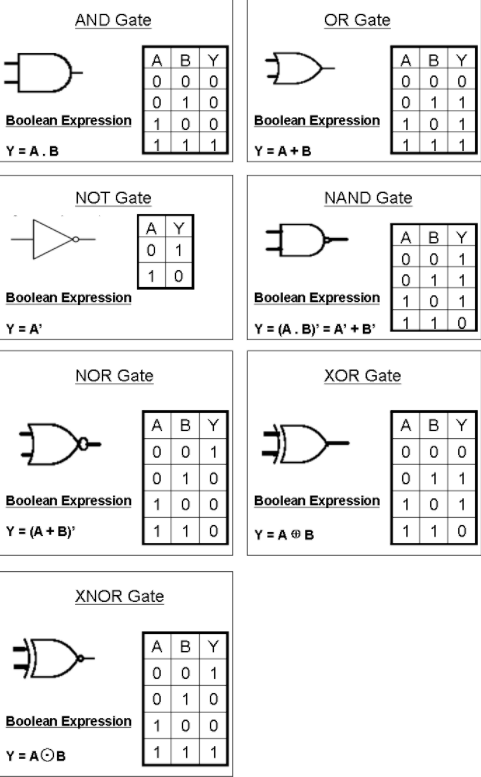
여기서 주목할 점은 A,B,Y 모두 1 bit 단위이며 0과 1만 나타내는 2진수라는 것을 알 수 있다.
Shift operation
이건 bit를 한 칸씩 혹은 N 칸씩 이동할 때 사용한다. 왼쪽, 오른쪽 모두 가능하며 그 방향은 값의 단위와 부호와 연관되기 때문에 매우 중요하다.
이 shift operation을 수행하는 하드웨어는 바로 'D Flip-flop'이다.
이에 대한 설명은 아래 포스팅을 참고하면 좋다.
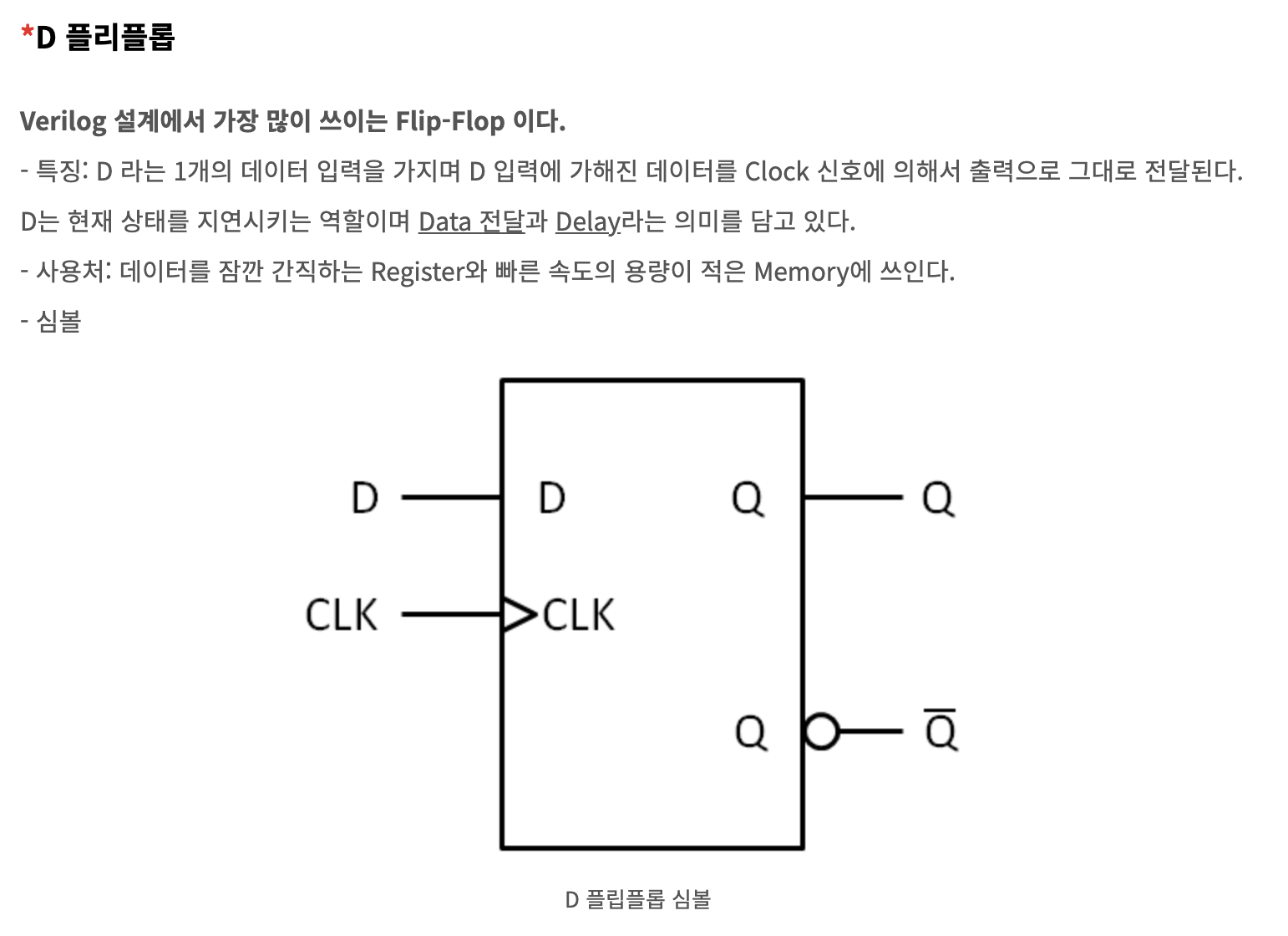
Verilog 설계에서 중요한 존재들 - 순차 논리 회로(Sequential logic circuits)_#Flip-Flop
순차 논리 회로(Sequential logic circuits) 현재의 입력과 기억 소자에 기록된 과거 출력들과의 조합에 의해 현재의 출력 값이 결정된다. 이 논리 회로에는 조합 논리 회로와 달리 '시간 개념'이 도
rubber-tree.tistory.com
산술(Arithmetic) 연산
Adder (Half-adder & Full-adder)
인간이 다루는 숫자 체계에서는 정수가 있고 음수까지 포함한 실수가 있다.
Adder라는 하드웨어를 통해 정수를 더하고 빼는 연산을 수행할 수 있다.
사실 Half-adder는 완벽한 가산기가 아니다. Carry-in이라는 올림수를 반영하지 못하기 때문이다. (Overflow라고도 한다.)
그래서 Half-adder 설명은 생략하고 Full-adder로 바로 넘어가면 아래 그림과 같다.
Full-adder는 Half-adder 2개에 마지막에 OR가 더해진 형태이다.
Input A,B가 있고 중간에 Cin(Carry-in)과 Output S와 Cout이 있다.
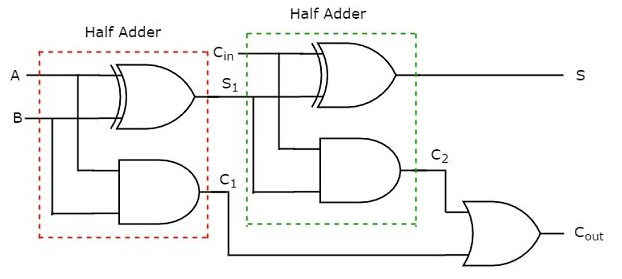
이게 A,B에 각각 1 bit 씩 들어가 긴 01011...의 조합 덧셈이 순차적으로 이루어진다.
우리가 흔히 아는 덧셈은 아래와 같은 구성된 하드웨어로 수행하는 것이다.
FA는 Full-Adder이다.
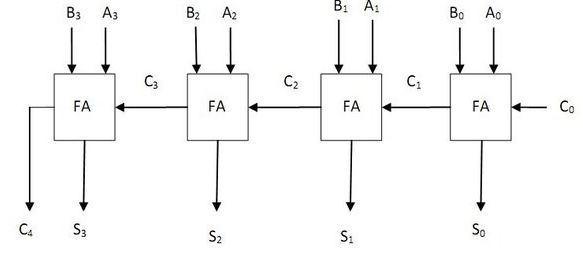
1100 + 0111 = 10011 으로 A가 1100, B가 0111 이며 Cout으로 1이 S는 0011이 나오는 것이다.
곱셈
곱셈을 하기 위한 전용 하드웨어는 없다.
위에서 언급한 Shift와 Adder의 조합으로 수행할 수 있기 때문이다.
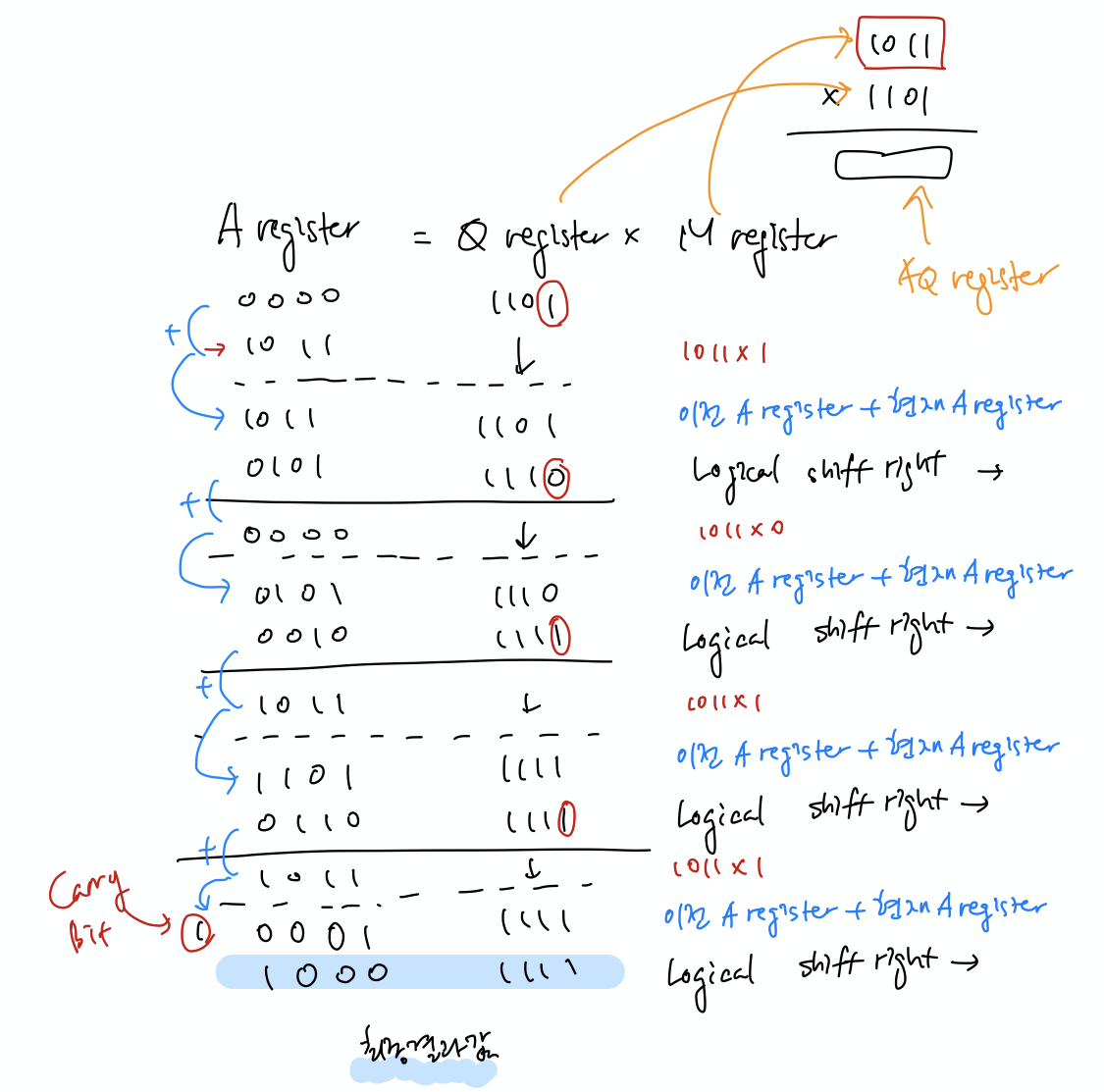
예를 들어, 1011과 1101을 곱해본다.
1011은 Q register에 있고 1101은 M register에 있다. 이 둘을 곱해 AQ register에 저장할 것이다.
Q register의 1 bit씩 읽어서 M register 만큼 곱해주고 이전 자신의 값과 더한 후, shift right를 해준다.
그리고 이 작업을 Q register 전체를 다 읽을 때까지 1 bit씩 수행한다.
그럼 신기하게도 우리가 손으로 계산하는 값과 일치한 값이 나온다.
음수 Signed 연산 (Feat. 2의 보수)
10 진수에서의 -10 x 5 의 연산을 2진수로는 어떻게 수행할까?
음수 표현은 '2의 보수'라는 개념을 사용한다. 이는 2진수로 음수를 표현하는 약속이다.
2의 보수
공식이라 잘 외우기만 하면 된다.
-10을 예시로 들면,
1) 10을 2진수로 표기한다. 1010(2).
그럼 4bit로 표현되는데
2) 표현되는 모든 bit에 1을 넣은 값에서 1010(2)을 뺀다.
1111 - 1010 = 0101(2).
이 것이 -10을 표현하는 2진수 이다. 그리고 이 방법을 2의 보수라고 부른다.
이렇게 10진수를 2진수로 변환하는 법, 2진수로 논리 연산, 덧셈, 뺄셈, 곱셈의 산술 연산하는 법을 알아 보았다.
이는 컴퓨팅 플랫폼 제어에서 아~주 기초적인 부분이므로 머릿속에 항상 저장해두고 어떠한 디지털 로직을 설계하더라도 상기시키는 것이 좋다.
'Digital Logic > 컴퓨터 구조' 카테고리의 다른 글
| Computer Architecture - Diagram (0) | 2024.10.13 |
|---|---|
| [VLSI] Very Large Scale Integraed Circuit (2) | 2023.12.31 |


댓글